이전 글에서 우리는 직사각형의 넓이를 계산하는 함수를 만들어 냈습니다. 직사각형은 2차원 물체입니다. 차원을 늘려도 우리가 만든 개념을 적용할 수 있을까요? 우리가 흔하게 접할 수 있는 상자를 상상해보죠.
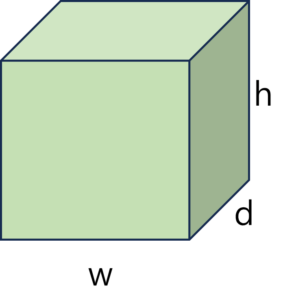
이 물체는 3차원 물체입니다. 이 물체를 구성하는 요소는 가로, 세로, 높이입니다. 그런데 문제가 생겼습니다. 직사각형의 높이와, 육면체의 높이가 서로 다른 것을 가르킵니다. 약자를 다시 정리해야 할 것 같습니다. 가로는 동일하게 w로 하겠습니다. 세로는 물체의 깊이를 의미하는 depth의 d로 정하겠습니다. 높이는 그대로 h를 사용하겠습니다.
이제 넓이를 계산할 때처럼 가로, 세로 길이는 그대로 두고 높이만 두 배로 늘려보겠습니다.
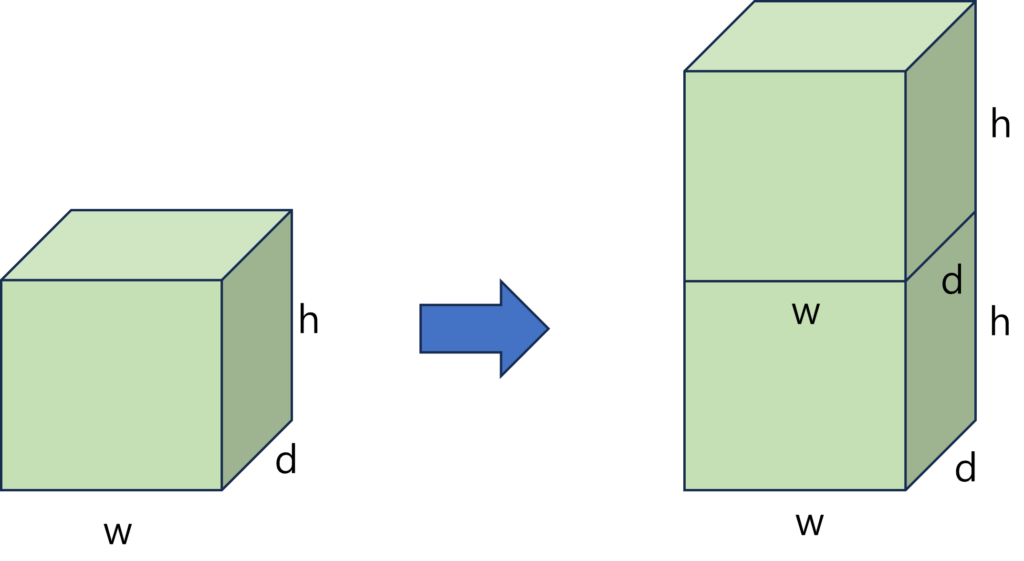
위 그림을 보면 원래의 상자 두 개가 생기니까 상자의 부피도 두 배로 늘어납니다. 만일 높이를 n배로 늘리면 상자가 n개 생기니까 상자의 부피도 n배로 늘어나겠죠? 가로의 길이만 늘려도, 세로의 길이만 늘려도 결과는 마찬가지입니다. 그렇다면 3차원에서도 세 가지 길이에 대해 n이 어떤 수인 가는 관계없이 부피에 대해서 참이 성립합니다. 이것을 요약하면 다음과 같습니다.
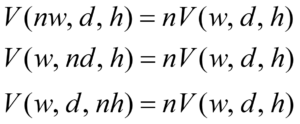
그리고 이 세가지 개념을 w, d, h라는 수 그 자체에 적용하면 다음과 같이 정리할 수 있습니다.
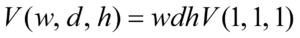
자 그렇다면 4차원에서는 어떻게 될까요? 안타깝지만 4차원부터는 그림을 그릴 수 없습니다. 하지만 n차원 공간이 어떻게 생겼고, 도형이 어떻게 그려지는지 알 수는 없지만, 도형이 차지하는 공간에 대해서는 동일한 논리를 적용할 수 있습니다. 그렇다면 다음의 식이 성립한다고 말할 수 있습니다.
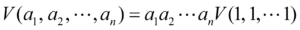
여기서 V는 n차원 공간에 존재하는 무엇이지는 잘 모르는 도형이 차지하는 공간의 크기(부피)를 의미합니다. 그리고 지금까지의 가로, 세로, 높이라는 용어는 사용하지 않겠습니다. 왜냐하면 n차원 도형이 어떻게 생겼는지는 상상할 수 없으니까요. n차원 도형의 각 변의 이름은 a로 통일하겠습니다. 그리고 여기에 숫자를 붙여서 각 변을 구분하도록 하겠습니다. 그리고 만일 각변의 길이가 a로 동일하다면 다음과 같은 식이 성립합니다.

여기서 V(1, 1, …, 1)은 n차원 도형의 단위가 됩니다.
지금까지 우리는 직사각형의 넓이를 일상적인 개념에서 출발해서, 식으로 요약하고, 일반화시켜서 결국 함수로 만들어 냈습니다. 그리고 단위라는 개념도 발견했죠.
직사각형의 넓이를 구하는 개념을 다른 곳에 응용해보자.
다음 공식은 우리가 수업시간에 배웠던 곱셈공식입니다.
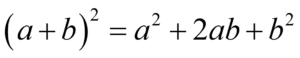
이것을 지금까지 우리가 만들었던 개념을 이용해서 새롭게 만들어보겠습니다. 다음과 같은 그림을 살펴보겠습니다.
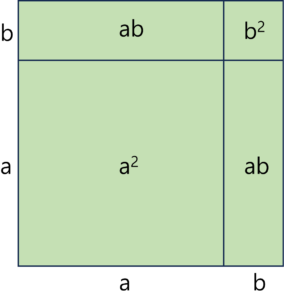
그림에서 가장 큰 정사각형의 넓이는 그 안에 포함된 모든 직사각형들의 넓이의 합과 같습니다. 이것을 식으로 요약하면 다음과 같습니다.
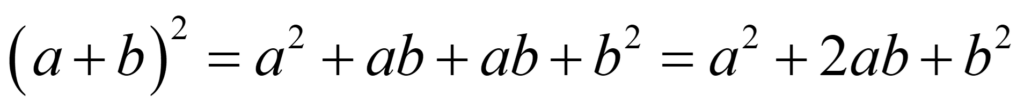
이번에는 직사각형의 넓이를 살펴보죠.
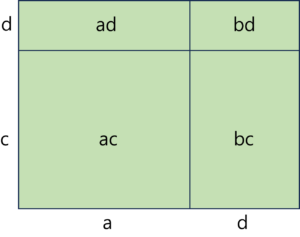
동일하게 가장 큰 직사각형의 넓이는 그 안에 포함된 모든 사각형들의 넓이의 합과 같습니다.
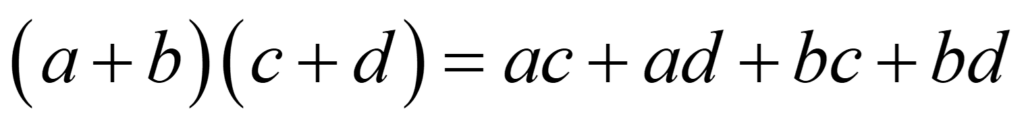
이것이 우리가 수업에서 배웠던 곱셈법칙의 정체입니다.