함수를 바라보는 또 다른 관점
이전 글에서 함수는 기계라고 했습니다. 하지만 수학책을 보면 함수를 집합을 이용해서 설명하기도 합니다. 이러한 관점에서 바라보는 함수는 관계를 의미합니다.
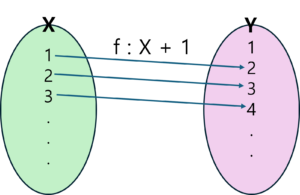
그림에서 함수 f는 X의 멤버들을 Y의 멤버들과 짝지어주고 있습니다. (f : X + 1)은 X와 Y의 관계를 설명해주고 있습니다. 그림을 보면 함수 f는 결국 X와 Y 사이의 관계를 표현하고 있습니다.
X와 Y의 멤버들은 정하기 나름입니다. 하지만 여기서 두 가지 지켜야 할 원칙이 있습니다. 첫번째 원칙은 X의 멤버들은 반드시 Y의 멤버 중 하나를 선택해야 한다는 것입니다. 두번째 원칙은 X의 멤버는 하나만 선택할 수 있다는 것입니다. 즉, X의 멤버는 양다리를 걸칠 수 없다는 것입니다. 물론 선택되는 Y의 멤버는 선택의 여지가 없으며, 함수 f에 의해 결정됩니다. 이러한 이유로 Y를 종속 변수로 부르기도 합니다. 비슷한 이유로 X는 독립변수라고 합니다. X의 멤버는 선택하는 주체이기 때문이죠.
함수의 역사
함수라는 용어를 처음 수학적 용어로 사용한 사람은 독일의 수학자 라이프니츠입니다. 라이프니츠는 함수를 다음과 같이 정의했습니다.
- 변수 x의 값의 변화에 따라 다른 변수 y가 정해진다면, y를 x의 함수라고 하자.
라이프니츠가 생각한 함수는 곡선을 그리는 그래프에서 x가 변할 때 y가 변하는 양을 설명하기 위한 개념이었습니다. 즉, 라이프니츠는 함수를 연속적인 변화를 설명하기 위해 사용했습니다. 이후, 요한 베르누이가 함수에 연속적인 변화와 대수식으로 표현하는 개념을 추가하였고, 함수에 식의 개념이 적용된 최초의 사례였습니다.
오일러는 함수를 두 수 사이의 관계를 나타내는 식으로 정의했습니다. 또한, 오일러는 f(x)라는 함수 기호를 최초로 사용했습니다. 라이프니츠는 함수를 표현하기 위해 단순히 기호 f를 사용했지만, 오일러는 여기에 괄호와 변수를 추가했습니다.
이때까지 함수는 연속적인 변화를 표현하는 개념이었습니다. 디리클레는 함수의 개념을 일반화시킨 최초의 수학자였습니다. 디리클레는 함수의 개념에서 연속, 변화, 식을 제거하고 다음과 같이 정의했습니다.
- 두 변수 x, y에 있어서 x의 값을 정하면, 그에 따라 y의 값이 정해질 때, y는 x의 함수이다.
이때부터 함수에서 변화, 식, 연속이라는 개념이 사라지고 두 변수의 특정한 관계로 함수가 정의되었습니다. 20세기에 이르러 부르바키라는 수학자 단체가 집합론을 바탕으로 함수를 정의했습니다. 부르바키는 함수를 다음과 같이 정의했습니다.
- 접합 X와 집합 Y에서 집합 X에 존재하는 모든 원소에 대하여 유일하게 대응되는 집합 Y의 원소가 존재한다면 y에서의 관계를 함수라고 한다.